El otro dia cuando xevi colgo el articulo de los dibujos de las motos y demas nada mas verlo me di cuenta de que es un articulo que parte de premisas falsas y lleva a malas interpretaciones po parte del que lo lee si no tiene claros los conceptos de los que habla. Pero no queria aclararlo hasta sentarme en el pc y ponerme a hacer unos dibujos en cad explicativos.
Para poder dar concluiones claras sobre la inclinacion de las motos deberia de tomar varias condiciones que hicieran de la comparacion algo creible, que vieramos como influyen las distintas variables. Voy a simplifacarlo todo lo maximo posible para que no sea muy duro el tema.
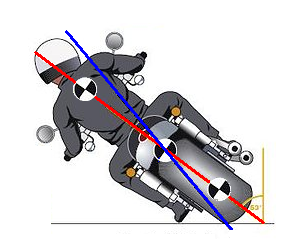
Primero tenemos que tener que estamos ante una composicion de dos fuerzas, una el peso y la otra la fuerza centrifuga.
P=m(masa)*a(que en este caso es la gravedad)
Fn(fuerza noral, por ser perpendicular)=m*an(aceleracion normal) donde an=v2(velocidad tangencial al cuadrado)/r(radio)
El calculo vectorial se puede hacer tanto matematicamente como graficamente. En los dibujos que os pongo he llamado P y V al vector Fn. Lo he llamado V porque la variable que mas nos interesa a todos de esta fuerza es la velocidad que llevamos al tomar la curva.
Supondremos siempre un mismo radio.
En el grafico 1 tenemos P=1 (unidad) y asi podemos ver como varia la velocidad en funcion del angulo para un mismo P. Se ve que a mayor angulo, mayor es la velocidad.
En el grafico 2 la constante pasa a ser la V y vemos como para generar el vector del angulo P aumenta cuanto menor es el angulo. Como conclusion sacamos que cuanto mayor es el P menor angulo se requiere para una misma velocidad.
En el grafico 3 toamos la inclinacion como elemento constante y vemos (en realidad no lo veis porque se me olvido poner el valor numerico, pero creerme XD) que la relacion entre V/P;V'/P' y V''/P'' es la misma. Esto nos lleva a la conclusion de que cuando los vectores P y V tienen la relacion adecuada para formar el angulo nos da igual en donde este el CG(centro de gravedad).
Visto esto nos damos cuenta enseguida que para hacer una comparacion real debemos introducir una nueva variable, el angulo. Y el angulo maximo nos lo determina el neumatico con todos sus limites y demas que seria una movida ponerme a explicar ahora (pero eso es otro tema) En fin que para estudiar la influencia del centro de gravedad debemos comparar una moto cuyo limite de inclinacion sea siempre el mismo.
En el ejemplo 4 vemos que el vector V es ligeramente superior para un CG mas alto. Esto se debe a que el angulo real entre el punto medio de contacto y el cg es ligeramente mayor que en los CG mas bajos.
En el ejemplo 5 probamos con un solo CG ysu desplazamiento en el eje vertical. Se puede ver claramente como el vector de V se incrementa de forma considerable.
En el ejemplo 6 hacemos el mismo desplazamiento en el eje horizontal y vemos que tambien aumenta el vector V, aunque lo hace menos que en el caso del desplazamiento vertical.
Por lo tanto, una moto mas ligera require un mayor angulo para entrar en la misma curva a la misma velocidad que una moto mas pesada.
Que descolgarse de la moto, por poco que sea, nos permitira tomar una curva a mayor velocidad o, y esto es lo que mas interesa, nos ayuda a reducir el riesgo de levar al limite nuestro neumatico ayudandole a mantenerse con la mayor superficie de contacto posible.
Despues hay que tener en cuenta que angulo permite el chasis que inclines tu moto y lo mas importante, si el neumatico lo aguantara.
Aqui hay otra razon mas para bajar el centro de gravedad. En el neumatico actuan las fuerzas antes vistas, el peso esta chupado de llevarlo al suelo, lo dificil es la Fn, en esta fuerza se aplica el brazo de palanca que hay desde el CG hasta el punto de apoyo. Cuano menor sea la distancia menor esfuerzo tangencial se le requerira a la goma.
Hasta aqui todo es off-topic, pues nada tiene que ver con las suspensiones, pero habia que decirlo.
Respecto a lo que dice ESTEBAN, en efecto, las orquillas invertidas aportan lo que dice, y precisamente lo hacen por lo que ya explique. Voy a poner un par de ejemplos un poco mas graficos.
Imaginad que teneis una barra gorda por un extremo y mas fina por el otro, que tenes que anclarla a la pared para colgar de ella un par de jamones. Que lado anclariais a la pared?
Ahora imaginaos a Chaplin apoyado en su baston, el baston se dobla, eso es lo mismo que pasa en las motos al frenar, lo unico que a otra escala y deslizandose una barra dentro de la otra.
Estructuralmente es claramente mas efectivo anclar al chasis de la moto la barra gorda ya que la flexion se reduce con el expesor, y reducir al maximo la seccion debil llevando el deslizamiento al punto mas favorable, el extremo inferior. Eso es la orquilla invertida.
Favorecer la transmision de fuerzas reforzando y haciendo mas eficaz la estructura mejora reparto de pesos, estabilidad en frenada, entrada en curvas, control de las frenadas y la acelarcion... en fin. Perdon por el toston.
Seguro que os han hecho falta al menos dos birras para llegar aqui asi que a la primera invito yo XD V'ssss
Perdon por las faltas que cometo muchas y cualquiera se lee esto dos veces.